泊松比是指材料在單向受拉或受壓時,橫向正應變與軸向正應變的絕對值的比值,也叫橫向變形系數,它是反映材料橫向變形的彈性常數。


自然界中的材料泊松比通常在0.1~0.5之間,如表1所示:
表1 常見材料的泊松比
| 橡膠 |
0.5 |
| 金 |
0.42~0.44 |
| 玻璃 |
0.18~0.3 |
| 鑄鐵 |
0.21~0.26 |
| 混凝土 |
0.1~0.2 |
| 鈦 |
0.26~0.34 |
| 鉛 |
0.43 |
| 大理石 |
0.2~0.3 |
| 鋁 |
0.33 |
| 銅 |
0.34 |
| 鋅 |
0.33 |
| 鋼 |
0.25 |
| 水 |
0.5 |
除天然材料之外,通過特殊結構設計,還可以實現零泊松比甚至是負泊松比結構,如下圖所示。
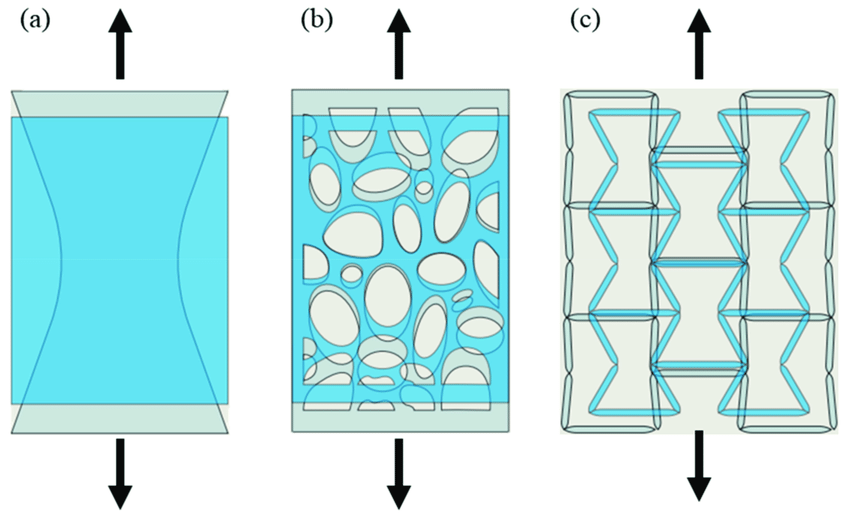
(a)正泊松比 (b)零泊松比 (c)負泊松比材料
對于各向同性材料,泊松比的定義比較清晰,但是對于復合材料,在不同的復合材料力學教材、手冊中,經常會看到以下兩種相反的互等公式:
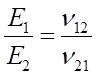
OR
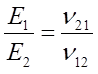
這是因為兩類公式中關于泊松比的定義是不同的。
一類復合材料力學教材中定義泊松比為:單軸應力σi作用在i 方向時,在j 方向引起的橫向變形的泊松比,即:
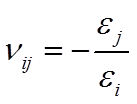
還有一類教材定義泊松比為 :單軸應力σj 作用在j 方向時,在i 方向引起的橫向變形的泊松比,即:
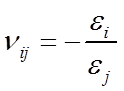
兩種定義本質上是一回事,只是符號表示不同,下角標i和j的順序相反,導致互等公式相反,也將進而導致剛度矩陣中各系數的表達不同:
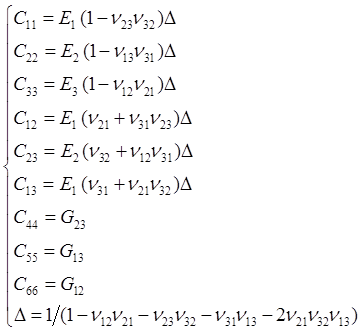
OR
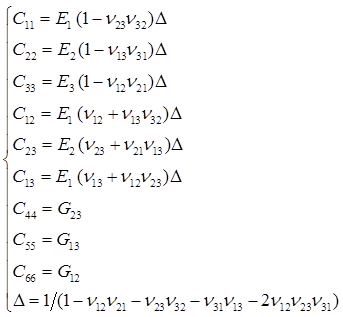
因此,自己在編寫計算程序的時候,需要注意模量和泊松比的數值范圍和互等關系。不同的人使用習慣不同,采用匹配的一套表達式即可,勿混用。小編習慣采用第一種泊松比定義方式。
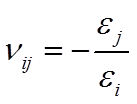
其對應的互等關系式如下:
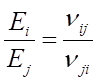
以面內楊氏模量及泊松比為例,通常對于復合材料單向板,E1>E2,采用上述定義方式時,ν12>ν21,為了避免交叉使用不同的泊松比和互等關系,可采用以下形式檢查自己編寫程序時泊松比的計算是否準確:
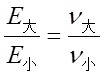
最后歸納一下兩種泊松比定義及對應的互等關系和剛度系數表達方式:
| 方式1 | 方式2 | |
| 泊
松 比 |
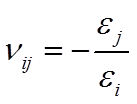
|
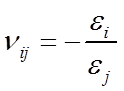
|
| 互
等 關 系 |
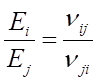
|
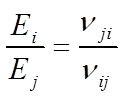
|
| 剛
度 系 數 |
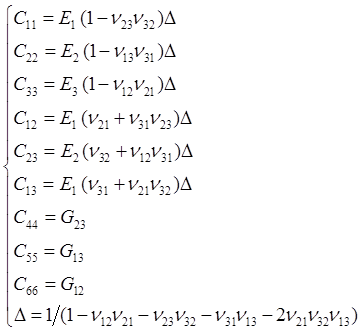
|
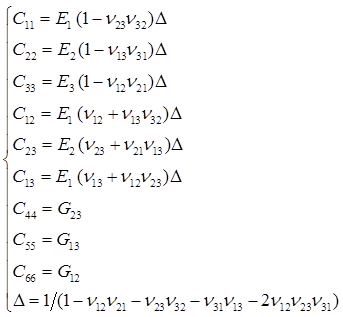 |
免責聲明:本文內容來自用戶上傳并發布,站點僅提供信息存儲空間服務,不擁有所有權,信息僅供參考之用。