很多時候，我們走在城市的街道上，低頭看路時，都會覺得為什么道路上，非機動車道上都有那么多圓溜溜的井蓋。雖然這也并沒有影響到太多通行，但是總覺得馬路上留著這么多坑坑巴巴的痕跡總不太美觀。于是善于觀察的同志們便會提出一個疑問？為什么大大小小的井蓋幾乎都是圓的，而別的形狀的井蓋卻很少見呢？

面試題刁鉆古怪的微軟

可能你們都知道這樣一個看似無厘頭的問題是一道經典的面試題目，據(jù)說這個問題可以從各個方面來進行回答。有的人說因為圓形井蓋容易運輸，且邊角不容易被磕磕碰碰，這是對的，圓形相對于三角形，正方形確實有這個優(yōu)點。有人說，圓形井蓋在受力時，會均勻地把力分散開來，不會在某個位置聚集，從而不容易導致邊緣破裂，這也是對的。還有人從哲學的高度來解釋，之所以用圓形井蓋比較多，那是因為本身井口就是圓形的啊，原來井蓋打造成圓形是天經地義的事情啊。

但是曉然菌還是想從數(shù)學的角度來考慮這個問題。

圓形井蓋

井蓋是維護城市生活正常運行的重要設施，萬一破碎或者被盜，對于該區(qū)域的人們來說影響都會很大，甚至會導致生命安全事故發(fā)生。防盜，現(xiàn)在早已不用金屬材質了，真的沒有多少經濟上的價值了。井蓋就算不被盜，那也不能直接從井口掉下去吧。沒錯，在數(shù)學上，大部分井蓋造成圓形，就是為了不讓井蓋掉進井里。

井蓋還是圓形居多

我們來做個試驗，我們用正三角形，正方形分別來充當井蓋，試驗翻轉一下看看能不能從井口掉下。這里要注意的是，實際上井口會比井蓋稍微大一丁點，這一丁點保證了井蓋可以圓潤地搭在井口內。不過這大的一丁點相比于整個井蓋的大小是微不足道的，于是在分析中可以忽略不計。

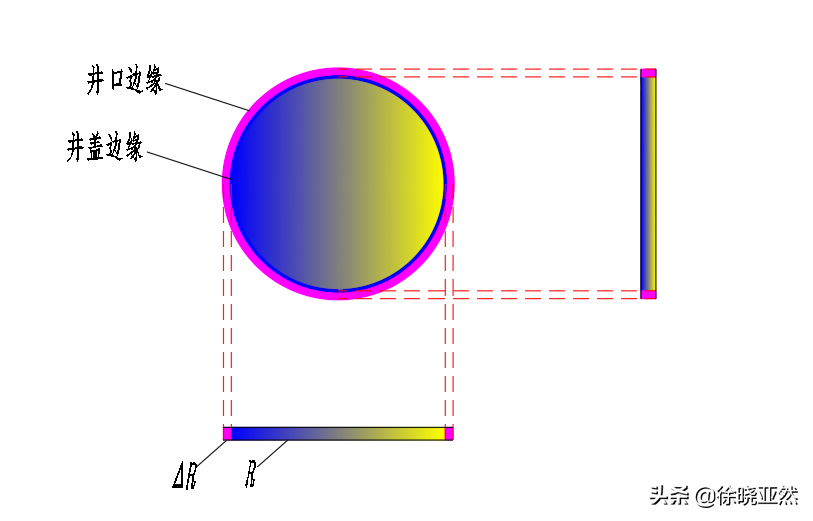
井口與井蓋的結構關系

對于三角形井蓋來說，當你準備把正三角形放入井口，我們以垂直將井蓋放進去，很快就發(fā)現(xiàn)，在放置的過程中假如偏轉一定的角度以避開那些最長的井蓋邊長觸碰到井口，很容易，三角形井蓋就穿過井口，且不會碰到井口邊沿的任何位置。我們可能一時半會搞不清是哪些長度決定著是否能夠落入井口，于是我們從各個角度來嘗試。

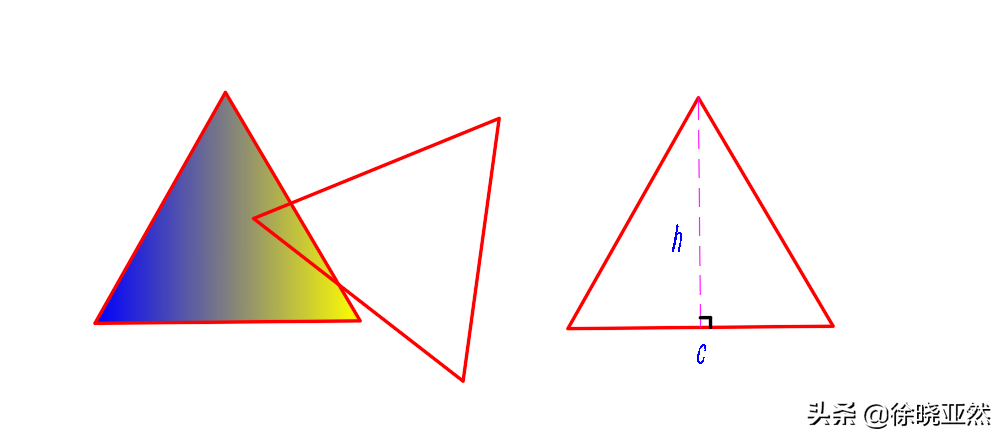
三角形井蓋不可行

很快我們發(fā)現(xiàn)根本原因是正三角形的高小于邊長，也就是說h

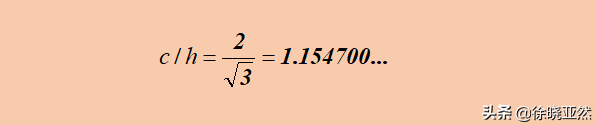
正三角形高與邊長的關系

既然三角形不行，那么正方形呢？

于是我們重復上面的操作，很快我們發(fā)現(xiàn)，還是可以在下落的過程中讓正方形完全落進井口里。不過這里的長度關系就不是上面的高與邊長的關系了。

正方形同樣不可行

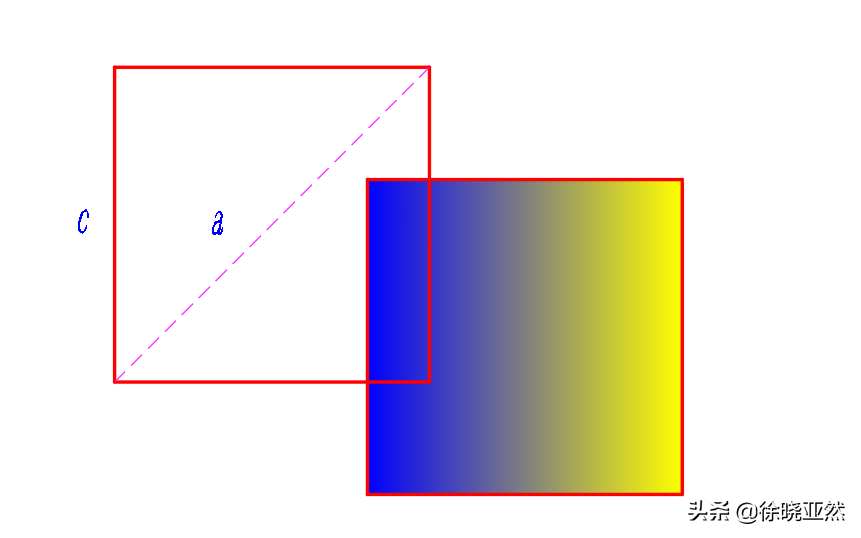
我們在下落過程中會旋轉角度，從多個方向嘗試過后，我們發(fā)現(xiàn)是因為正方形的對角線大于其邊長，也就是a>c。所以每次我們總是能夠把正方形翻轉角度使得它可以在對角線長度以內落進井口。

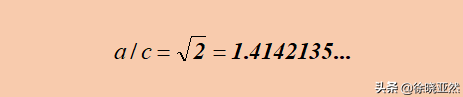
正方形邊長與對角線關系

那我們換成矩形呢？其實是一樣的啊，因為勾股定理存在，對角線的長度適中都會比任何一個邊要長。所以矩形也可以完全不觸碰井蓋邊緣就落進井底。

這個時候我們嘗試了三角形，正方形，接下來，我們再來考察一下正五邊形。有了前面兩種情況的分析，我們發(fā)現(xiàn)，井蓋是否能夠落入井口的根本原因是對角線與高的長度關系。因此我們不必再做實驗進行分析，我們畫出正五邊形來，通過理論來計算一下正五邊形對角線和高的關系。

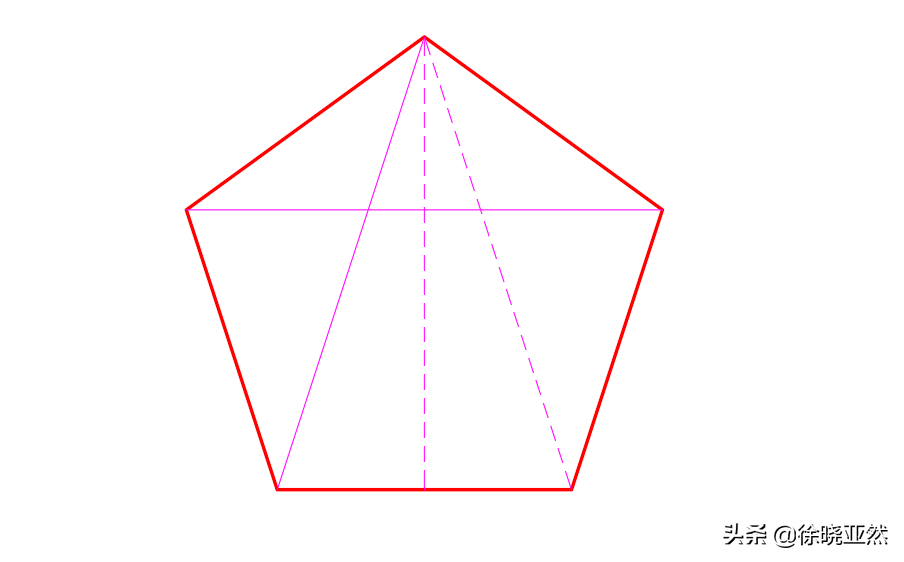
正五邊形

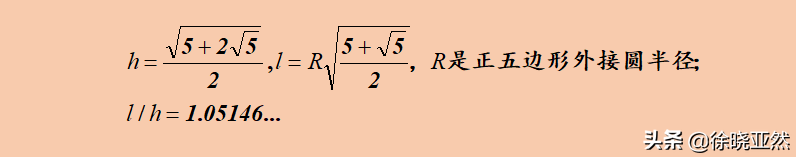
正五邊形對角線與高 的關系

通過對正五邊形的考察，從一開始我們列出的等式可以發(fā)現(xiàn)這個問題的本質，我們發(fā)現(xiàn)，當邊的數(shù)量越多時，對角線和高就越接近。

當高與對角線的長度差距越大時，越容易掉落井口里，因為在落下的過程中，可以翻轉的角度和空間越多。當高與對角線的長度逐漸逼近時，此時在落下的過程中，翻轉角度就顯得不是那么容易實現(xiàn)了。

推廣到無窮多邊形時，滿足條件的井蓋自然是圓形的

于是，我們很自然地推廣到，當邊數(shù)無窮大的時候，也就是圓時，此時，高和對角線會越來越接近，到最后就分不清多邊形的高和對角線了。因此我們無論怎么翻轉圓形井蓋，圓始終都會與井蓋牢牢卡住，從而掉不進去。

那么現(xiàn)在問題來了，是不是只有圓形井蓋落不到井口下面去？當然不是，圓形并不是能否掉落井蓋的根本原因，根本原因在于那句話。

只要在翻轉圖形的過程中，圖形寬度始終保持一致即可。

圓形在任何角度上觀察，圖形占據(jù)的寬度都是相同的，這樣就導致了圓形在下落過程中，翻轉動作以規(guī)避井口的操作無效。我們把這種性質叫作等寬性，只要我們能再找出一種滿足等寬性的圖形，那就可以新發(fā)明一種井蓋了。

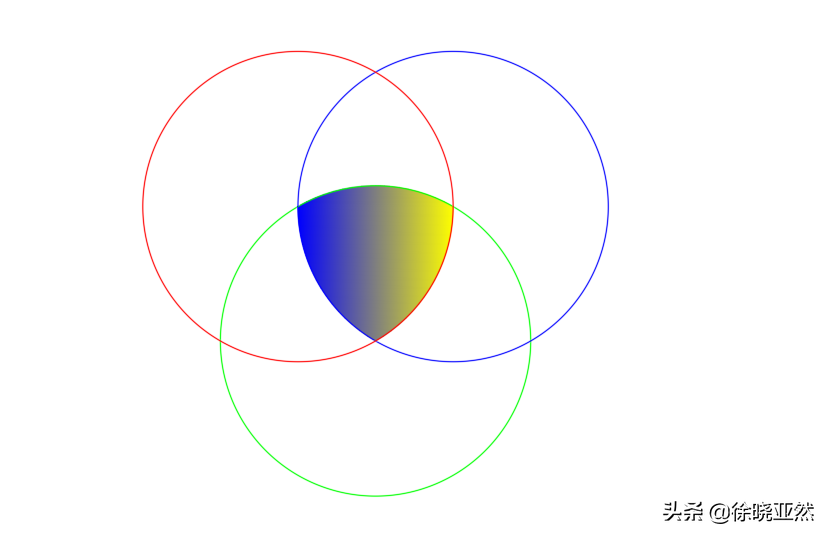
萊洛三角形畫法

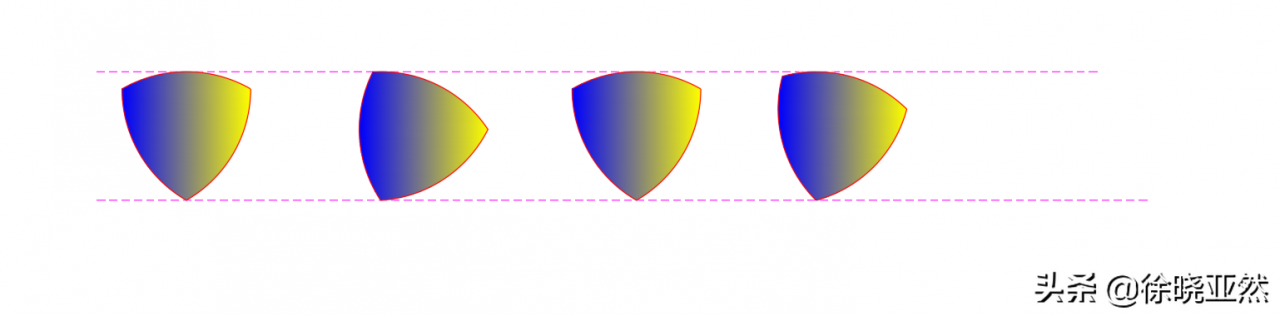
萊洛三角形滾動

你可能在某些場合見過下面這樣的圖形。畫法也很簡單，將3個等半徑的圓以對稱中心120度間隔相交而成的圓弧三角形，這種三角形看似胖胖憨憨，但是卻有著不同尋常的性質。你用一對平行線在任何角度去測量其寬度，寬度都是一致的。這種三角形叫作萊洛三角形，這個定義由十九世紀的德國工程師Franz Reuleaux命名。也正是基于這個性質，萊洛三角形是井蓋問題一個經典答案。

德國工程師 弗蘭茲 萊洛

這個看似簡單的胖三角，是最簡單的等寬曲線，想象一下這個神奇的性質。在一個平面下安裝幾個這樣的萊洛三角形作為輪子，任你移動平面，你也不會感覺到平面會有絲毫的起伏不穩(wěn)。這個時候有同學又在疑問了，既然萊洛三角形任意移動寬度始終一致，那可不可以做車輪呢？答案是幾乎不可以。為什么呢？

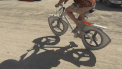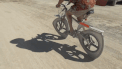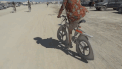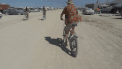
騎上萊洛三角形為輪子的自行車

雖然說萊洛三角形在任何旋轉情況下，圖形的寬度不會改變，然而其旋轉中心點卻在實時波動。想象一下，如果騎自行車用萊洛三角形做車輪，前后輪軸承的位置就是旋轉中心，而這個中心總是忽高忽低，這樣這個車可以騎，但是在平面上卻有著騎蹺蹺板的感覺，仿佛感覺不是特別美好。不過有人卻從這種怪異的胖三角形里得出靈感來，創(chuàng)造了一件偉大的發(fā)明。

滾動萊洛三角形時，平面絲毫不動

德國人菲加士·汪克爾注意到萊洛三角形在直線上翻轉時，上下寬度總是一樣，旋轉中心是中間區(qū)域的一個小圓形。如果以萊洛三角形為轉子，在這個轉子中間再加上偏心軸，再構造一個特定的腔體，不就可以規(guī)避掉旋轉過程中心波動問題，并且還可以使得轉子持續(xù)轉動下去做功了么？

轉子發(fā)動機發(fā)明人 菲加士·汪克爾

然而萊洛三角形是有3個明顯的角的，這3個尖角在實際加工過程中是不容易實現(xiàn)的，而且轉子在高速轉動時，必然會帶來更多的磨損，因此用尖角是不可行的。于是汪克爾采用了變形了的萊洛三角形，也就是讓一個圓在原先的萊洛三角形邊上滾動一圈，以這個圓的最大邊緣的軌跡重新構造一個改進的萊洛三角形。可以想象，若這個外圍的圓相對于萊洛三角形的直徑越大，最后的軌跡就將越圓滑。我們仍然可以證明這樣的曲線是等寬曲線，因此用這樣的圓滑萊洛三角形來作為發(fā)動機轉子將更加適合。

轉子發(fā)動機模型

理論上可行了，但是在實際加工制造過程中，汪克爾還要克服各種各樣的問題才有可能讓轉子發(fā)動機成為現(xiàn)實。1927年，汪克爾在經過無數(shù)次試驗過后，基本上解決了諸如氣密性和潤滑等的一系列技術問題。1967年，日本東洋公司第一次把轉子發(fā)動機批量裝在汽車上，后來讓轉子發(fā)動機大放異彩的還是執(zhí)著的馬自達公司，幾十年來一直鍥而不舍研究。馬自達公司在1991年6月23日創(chuàng)造了歷史，在當天進行的勒芒24小時耐力賽上，搭載轉子引擎的馬自達787B賽車以領先第二名兩圈的巨大優(yōu)勢奪冠！

創(chuàng)造歷史的馬自達神車 787B

雖然轉子發(fā)動機也有燃燒不充分，污染嚴重，油耗高等缺點，但是它卻跟傳統(tǒng)的活塞發(fā)動機有著巨大的不同，小小的體積可以迸發(fā)出驚人的動力。它的出現(xiàn)的確給人們在動力的追求上帶來了耳目一新的感覺，原來發(fā)動機還可以長這樣。

掃地機外形也是萊洛三角形

為什么井蓋基本上都是圓形的？這個問題真的可以有千百種答案，每一種答案都可以是讓人信服的。我們單純從數(shù)學角度來出發(fā)，卻引申出了如此多的經典結論，實在是出乎人們的意料。知道了井蓋的原理之后，我們發(fā)現(xiàn)了萊洛三角形，從萊洛三角形的特點中我們提出了等寬曲線的概念，再到后面將萊洛三角形實踐化造出了轉子發(fā)動機。

相信井蓋的科學還會一直延續(xù)下去的。